The earliest Poisson distribution polymers were synthesised by the group of Szwarc and reported in both JACS and Nature in 1956, with the JACS communication having all the actual data and the Nature communication being an advertisement to the non-chemists. If you ever want to see the difference between publications then and now, read them. There is essentially no data contained in them.
Szwarc’s interest was in forming block copolymers, and the Poisson nature of the distribution was incidental. However, to get pure block copolymers without parasitic homopolymers we need to achieve the similar conditions as those to get the Poisson distribution. To get a Poisson distribution four criteria need to be fulfilled, namely:
- “Instantaneous” initiation of polymerisation (ki >> kp)
- Irreversibility of the propagation reaction
- Homogenity of the polymerisation system
- Lack of termination or transfer reactions during propagation
A system fulfilling such criteria is called “living”, although this was a rather poor choice of words by Szwarc (Nylon-6,6 is “living” in the sense the chain ends are still active but it is not a Poisson distribution polymer). Very few polymerisation systems are truly living, and the majority are anionic polymerisations of a discrete set of monomers (mainly styrene, methyl methacrylate, ethylene oxide).
Now the advantage anionic polymerisation has over cationic is that with cationic polymerisation it is usually easy to eliminate a proton (H+) to form an unsaturated endgroup (typically an alkene). Electronically it is very difficult to eliminate a hydride. However, in anionic polymerisation if the incoming monomer has a δ+ proton (or other electrophilic group) then there is a chance of transfer to monomer. This is a main limiting factor governing which of the anionically polymerisable monomers give Poisson distributions (assuming solubility).
Now, my personal interest is in water-soluble polymers with pharmaceutical use, and the only water-soluble polymer which can be synthesised with a Poisson distribution (but typically isn’t) is poly(ethylene oxide) (aka poly(ethylene glycol) aka PEG). There are however other polymers which can be made with very narrow molecular weight distributions, if not Poisson. The main two are poly(2-ethyl-2-oxazoline) and poly(hydroxymethacrylamide). I have synthesised both of these, although the HPMA polymerisation was via standard free-radical polymerisation, not RAFT.
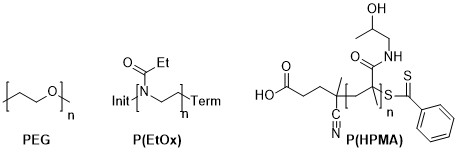
Figure 1: Structures of PEG, P(EtOx) and RAFT polymerised P(HPMA)
My main effort for the last few years has been controlling the MWD of P(EtOx), which was successful. This will be discussed in the manuscript I’m currently (re)writing.
The other contender is P(HPMA), which is essentially the domain of Prof. Jindřich Kopeček and his “academic family”. The presence of a hydroxyl group in the side-chain gives the polymer its water-solubility, but also precludes living anionic polymerisation. Control of the polymerisation is achievable by RAFT, and was reported in 2005. Like any RAFT the polymerisation is not truly living but is “quasi-living”. However it is living enough.
Now RAFT is a controlled radical polymerisation. At the most basic level these polymerisations are “pseudo-radical”. Whilst the polymerisation is a radical addition to a double bond, the radicals can best be described as “masked”. The dithiobenzoate at the ω-terminus is only quasi-stable, and undergoes homolytic cleavage to form a radical, but rapidly recombines to reform the endgroup. If however an collision with a monomer alkene occurs in that period then an addition reaction occurs. Of course, if a collision with another end in the active state occurs then radical-radical recombination will occur and the polymer will be terminated. This is an unavoidable process, but can be suppressed by dilute solutions and avoiding high conversions.
RAFT and other controlled radical polymerisations look brilliant for medium sized polymers (a few hundred repeat units) but as the MW is increased they deviate significantly from the Poisson distribution. At the lower end since initiation is from a normal radical source like AIBN, they can suffer from “slow initiation”, and also deviate from the Poisson distribution.

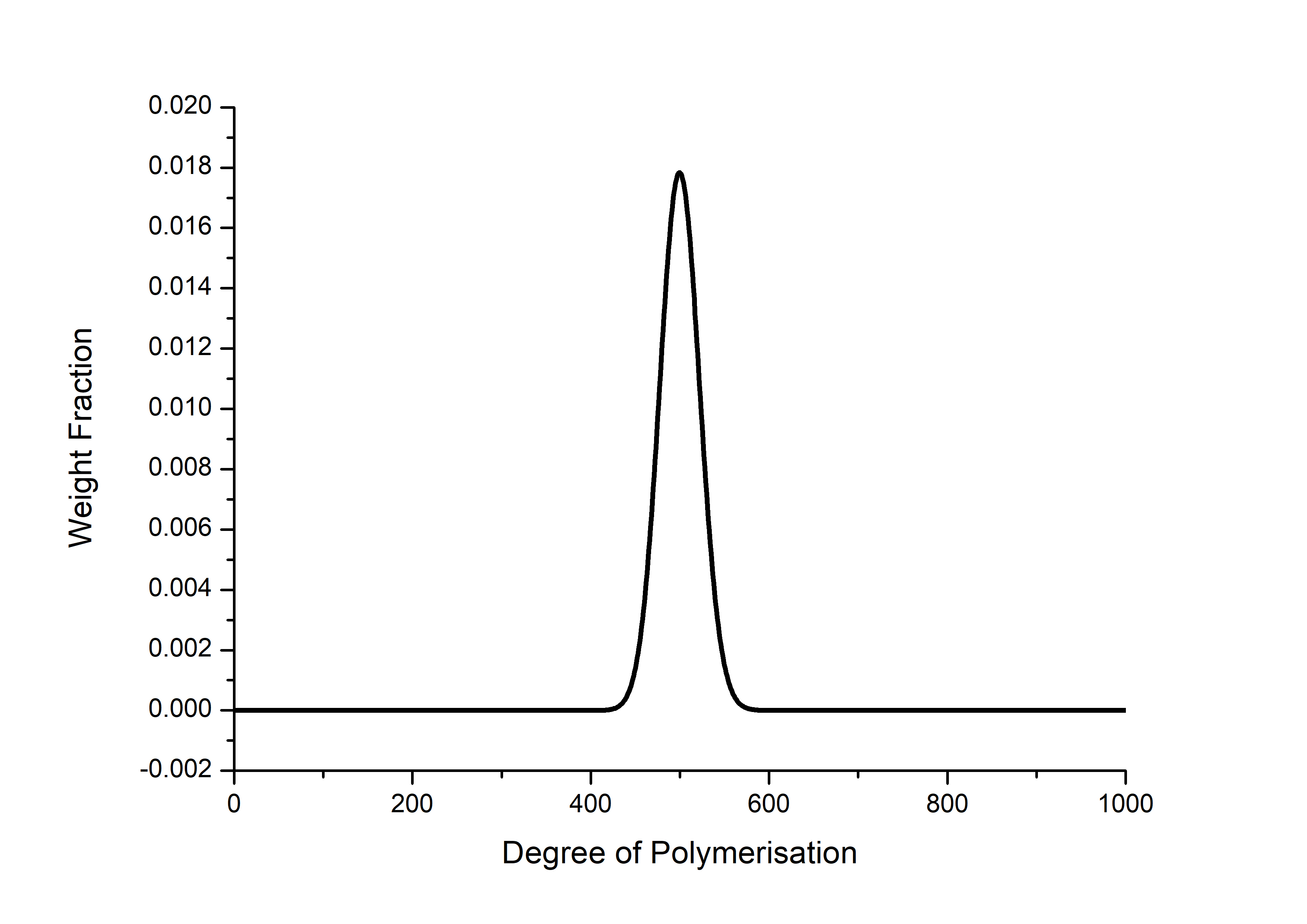 Figure 1: Theoretical molecular weight distribution of a DP = 500 polymer
Figure 1: Theoretical molecular weight distribution of a DP = 500 polymer